2023福建高考切线

福建高考是全国高考中的重要一环,每年都吸引着数以万计的考生参加。在数学科目中,切线是一个重要的概念,尤其是圆的切线。本文将详细介绍2023福建高考切线(圆的切线的性质定理),帮生更好地理解和掌握相关知识。
切线的概念
切线是几何学中的一个重要概念,指的是与曲线相切且只有一个公共点的直线。对于圆来说,切线是与圆相切且只有一个公共点的直线。切线的性质定理是研究切线与圆的关系的重要工具,它们可以帮助我们求解与切线相关的问题。
切线的性质定理
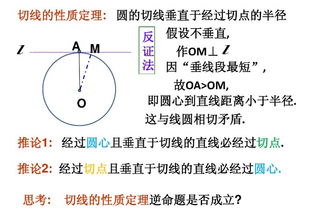
定理一:切线与半径垂直
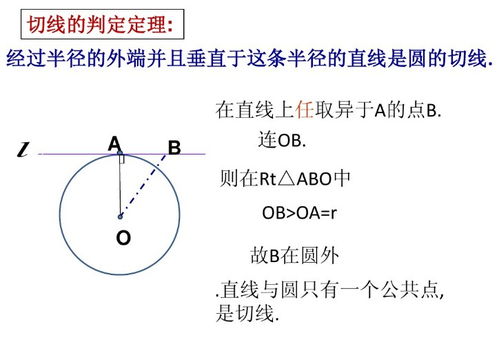
圆的切线与通过切点的半径垂直。
根据这个定理,我们可以得出切线与半径的关系。当切线与半径垂直时,切线与半径之间的夹角为90度。这个定理在解决与切线和半径相关的问题时非常有用,可以帮助我们确定切线的方向和位置。
定理二:切线的长度
切线的长度等于切点到圆心的距离。
这个定理可以通过勾股定理来证明。假设切线的长度为x,切点到圆心的距离为r,则根据勾股定理,可以得出x²+r²=(半径)²。通过这个定理,我们可以求解切线的长度,从而解决与切线长度相关的问题。
定理三:切线与切线的关系
如果两条切线与同一个圆相切,那么这两条切线的切点和切线之间的夹角相等。
这个定理可以通过相似三角形的性质来证明。假设两条切线分别与圆相切于A、B两点,切点与切线之间的夹角分别为α和β,则根据相似三角形的性质,可以得出α=β。这个定理在解决与切线之间的夹角相关的问题时非常有用。
切线的应用
应用一:求解切线方程
切线方程是指过给定点且与曲线相切的直线的方程。对于圆来说,切线方程可以通过切线的性质定理来求解。
假设圆的方程为(x-a)²+(y-b)²=r²,切点为(x₀,y₀),切线方程为y=kx+m。根据切线与半径垂直的性质,可以得出k=-(x₀-a)/(y₀-b)。再根据切线的长度定理,可以得出m=y₀-kx₀。通过这两个公式,可以求解切线方程的系数k和m。
应用二:求解切线与切线的交点坐标
当两条切线与同一个圆相切时,我们可以通过切线的性质定理求解它们的交点坐标。
假设两条切线的方程分别为y₁=k₁x+m₁和y₂=k₂x+m₂,圆的方程为(x-a)²+(y-b)²=r²。根据切线与切线的关系定理,可以得出k₁=k₂。再根据切线的长度定理,可以得出m₁-m₂=±2r√(k₁²+1)。通过这两个公式,可以求解切线与切线的交点坐标。
切线是圆的重要性质之一,在几何学中有着广泛的应用。掌握切线的性质定理能够帮助我们解决与切线相关的问题,特别是在解决圆与切线的交点、切线方程等问题时非常有用。希望本文对考生们在2023福建高考中的数学备考有所帮助。